Harmonic Trajectories in the Tonnetz
An introduction to Symbolic Representations, Tonnetze, and Trajectories.
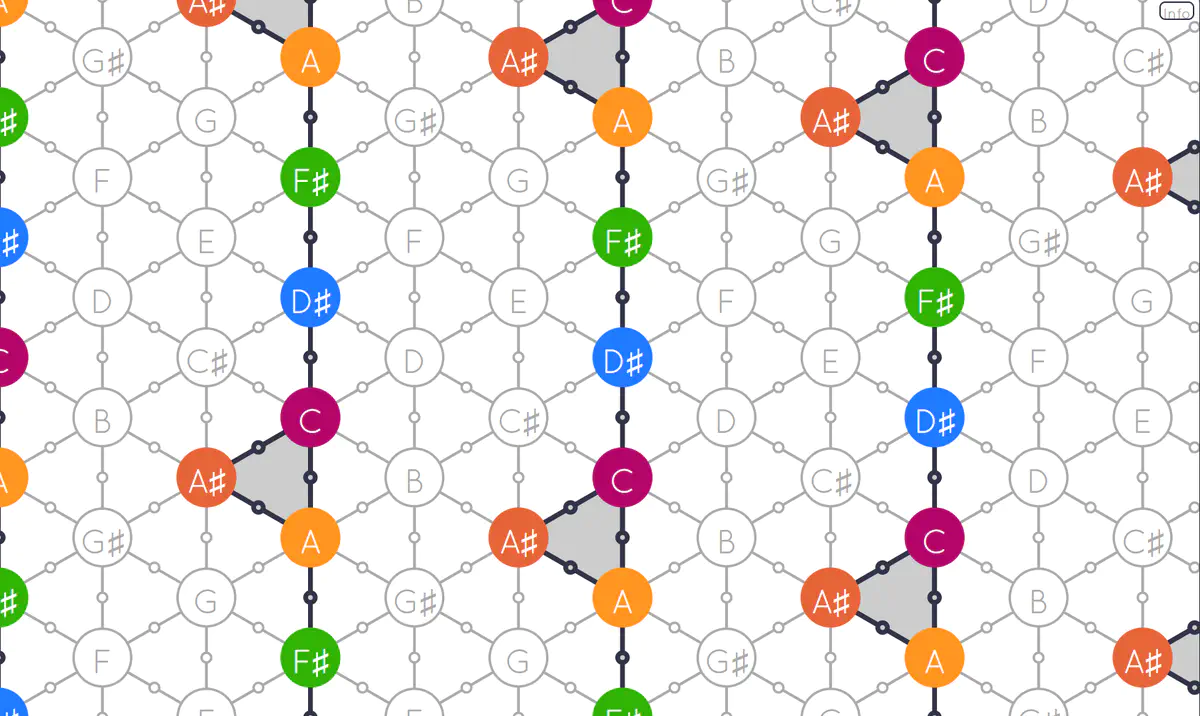 Tonnetz 1-2-9
Tonnetz 1-2-9Harmonic Trajectories in the Tonnetz
Introduction
The Neo-Riemannian Tonnetz is a way of visualizing musical relationships between chords. It was developed by music theorists to help understand how chords can transition smoothly from one to another.
Imagine a grid or network of interconnected points. Each point represents a different chord. The horizontal lines connect chords that are closely related, while the vertical lines connect chords that share similar tonal qualities.
The Tonnetz is based on the idea that chords can be transformed or changed into one another through small movements. These transformations are represented by diagonal lines on the Tonnetz. For example, a chord can be transformed into another chord by changing one note at a time, moving in a specific direction on the grid.
By studying the Tonnetz, musicians and theorists can analyze chord progressions and see how different chords are related to each other. It provides a visual representation of the harmonic possibilities and helps to explain the underlying structure of music.
In simple terms, the Neo-Riemannian Tonnetz is a grid that shows how chords in music are connected and can be transformed smoothly from one to another. It helps musicians and theorists understand how chords fit together and how they can create pleasing transitions in music.
Overview
PLR operations, also known as Parallel, Leading Tone, and Relative operations, are a set of chord transformations used in music theory. These operations help musicians understand how chords can be changed while maintaining a similar musical function.
Parallel operation: This operation involves changing a chord to another chord with the same root note but a different quality. For example, if you have a major chord, you can transform it into a minor chord by lowering the third note. This maintains the same root note but gives a different emotional quality to the chord.
Leading Tone operation: The leading tone refers to the seventh note of a major scale, which is one step below the tonic note. In this operation, a chord is transformed by changing the root note to its leading tone. This creates a sense of tension and a desire to resolve back to the tonic chord. For example, if you have a C major chord, you can transform it into a B diminished chord by changing the root note to B.
Relative operation: This operation involves changing a chord to another chord that shares a similar tonal quality but has a different root note. For example, if you have a C major chord, you can transform it into an A minor chord by changing the root note to A. The relative operation allows for smooth transitions between chords that have a related sound.
These PLR operations provide musicians with tools to transform chords while maintaining certain musical characteristics. By understanding these operations, musicians can create interesting chord progressions, establish tension and resolution, and explore different harmonic possibilities in their music.
The PLR operations are the foundation of the Tonnetz.
These operations/ transformations are the principal transformations of the Neo-Riemmanian theory which was mainly conceived by David Lewin (1933–2003). The mirror process is relative to the chord intervalic relations not the position of the shape in the circle.
PLR as Group Operations
The PLR group acts simply transitively on the set {$ n_M,n=0…11$} $\cup$ { $n_m,n=0…11 $} of the 24 major and minor triads, where $n_M$ (resp. $n_m$) represents a major (resp. minor) triad with root n in the usual semi-tone encoding of pitch classes.
It is isomorphic to the dihedral group D24 of order 24, and is generated by the following two transformations.
The transformation $L: \mathbb{Z} _{24} \to \mathbb{Z} _{24}$ is called the leading-tone operation, and is such that:
$$
L(n_M)=(n+4)_m \textrm{ and the complementary } L(n_m)=(n+8)_M
$$
The transformation $R: \mathbb{Z} _{24} \to \mathbb{Z} _{24}$ is called the relative operation, and is such that:
$$ R(n_M)=(n+9)_m \textrm{ and similarly the complementary } $$
Though not a generator, the operation $P=(RL)3R$, called the parallel operation, is often considered, and is such that $P(n_M)=n_m$
Trajectories in the Tonnetz
The trajectory is defined as a path $\mathcal{X} $ in the Tonnetz $T$, i.e. an ordered list of positions in the space $T$.
Let us investigate some basic scenarios for trajectory construction.
Placing the first note in the Tonnetz has no bearing on the descriptors we ultimately compute,
so we can simply pick an arbitrary position. Now we consider the case where we have to place two notes:
one of them is placed as in the previous case, and the second one is placed according to a criterion
depending on a distance measure. To this end, we define a function $dist: \mathbb{Z} _{12} \times \mathbb{Z} _{12} \to \mathbb{N}$,
which assigns to the pitch class representation of notes, $x$ and $y$, their distance according to a given Tonnetz as:
\begin{equation}
dist(x, y) =
\begin{cases}
0 & \text{if } x=y \
1 & \text{if } (x-y)\in T \lor (y-x)\in T \
2 & \text{otherwise}
\end{cases}
\end{equation}
Note that, $ dist(x, y) = dist(y, x) $.
By abuse of notation, from now on when referring to notes or chords we automatically consider the numerical representations of their pitch class (PC). They are defined with integer notation, where $C=0$, $C#=1$, $D=2$, etc. Accordingly, chords are PC sets.

Two notes $x, y$ are neighbors if $dist(x, y)=1$. Thus, in the case where two notes are neighbors we find which kind of interval they form and to which Tonnetz axis this interval corresponds. In the case where $dist(x, y)=2$, we define a positioning according to a shared neighbor. For example, in Tonnetz $T( 1, 2, 9)$, the placement of note E in relation to note C is computed using the shared neighbor D: D is first placed in relation to C, then E is placed in relation to D. This example is illustrated in Figure 1 (horizontal axis). The intermediate neighbors are denoted in red.
Given a note $x$ and a position $p$ and a fixed Tonnetz $T$, let $\pi(x, p)$ be a positioning function for $T$ which, from the reference position $p$, places the note $x$ as described above.
We now move on to chords, which we will demonstrate on the simple case of a triad but generalize as well to chords of any size. In Figure 1 a C major chord is represented in 4 different Tonnetze, $T(1, 3, 8)$, $T(1, 2, 9)$, $T(3, 4, 5)$ and $T(2, 3, 7)$. From this representation we can see that in $T(3, 4, 5)$ the chord forms a connected graph while in the other cases the graph is disconnected. In all representations, we place the note $C= 0$ %\Isa{la notation PC n’est pas introduite} at point $(0, 0)$. From there, we place the other notes based on the Tonnetz intervals and periodicity. For example, we first need to find if E and G are neighbors of C in Tonnetz $T$. For this we consider the following function, which gives the neighbors in the chord $X$ of note $y$ according to Tonnetz $T$: \begin{equation} neigh(y, X, T) = { x\in X \mid dist(y, x)=1 \text{ in } T} %, & \text{otherwise} \end{equation} In the C major scenario, E and G are neighbors of C in Tonnetz $T(3, 4, 5)$ so we can easily find their place in $T$. We define a function which takes a chord $X$ and a position $p$ in a fixed space $T$ and assigns positions to all notes of $X$ as follows: \begin{equation} f(X, p) = { \pi(x, p) \mid x \in X } \end{equation}
If a chord does not strictly consist of neighboring notes, we first place notes which are neighbors of $y$, then we attempt to place the remaining notes according to the newly positioned notes, repeating until no more notes can be placed. For a note $y$ with corresponding position $p_y$, a chord $X$ and a Tonnetz $T$, first finds the neighbors of $y$ and then the neighbors of each neighbor of $y$ in $T$, etc. If some notes remain to be placed, then one of the remaining notes is placed in relation to an arbitrary already placed note, and the process is repeated.
Chord Trajectory Construction
This process, detailed in Algorithm 1, ensures a methodical approach to positioning each note within a chord on the Tonnetz grid. By iteratively placing neighboring notes, the algorithm builds a coherent and connected representation of the chord. If any notes remain unplaced after the initial neighbor placements, the algorithm continues by arbitrarily positioning the remaining notes relative to those already placed. This iterative process guarantees that all notes find their appropriate positions on the Tonnetz.
Algorithm 1: Placement of the First Chord
- Input: A chord ( X ) and a Tonnetz ( T )
- Result: A set of placed notes
Steps:
- Choose an arbitrary note ( x ) from ( X ) and assign it a position ( p_x ).
- Initialize
placedwith ( {(x, p_x)} ). - Initialize
to_placewith ( X \setminus {x} ). - While
to_placeis not empty:- While there exists a note ( x ) in
placedand a neighbor ( y ) into_place:- Place ( y ) in relation to ( x ) and update
placedandto_place.
- Place ( y ) in relation to ( x ) and update
- If no neighbors are found, place a remaining note ( y ) relative to an arbitrary note ( x ) in
placed.
- While there exists a note ( x ) in
This algorithm ensures that the positioning of each chord is systematic and consistent, leveraging the geometric structure of the Tonnetz.
Extending to Chord Sequences
For sequences of chords, the placement must consider the relationships between consecutive chords. The trajectory ( \mathcal{X} ) for a sequence of chords ( [C_1, C_2, \ldots, C_k] ) is built by extending the positioning strategy to maintain coherence across the entire sequence.
Given a chord ( C_n ) with known positions for ( C_{n-1} ), the positioning for ( C_n ) is determined by selecting optimal reference points from ( C_{n-1} ) to ensure a compact representation. This process is repeated for each chord in the sequence.
Example: I-IV-V-I Progression in C Major
Consider the sequence I-IV-V-I in C major:
- Chords: C major, F major, G major, C major
- Pitch Class Sets: ({0, 4, 7}, {5, 9, 0}, {7, 11, 2}, {0, 4, 7})
- C Major: Position C at (0,0) and place E and G accordingly.
- F Major: Position F major relative to C, using common note C as a reference.
- G Major: Position G major relative to both F major and the subsequent C major to find the most compact placement.
- C Major: Reposition C major with reference to G major.

Compliance Function and Compactness
To determine the best Tonnetz for a given piece, the compliance function evaluates the compactness of trajectories across different Tonnetz configurations. The compliance predicate ensures that each chord is represented as a connected graph within the Tonnetz. The trajectory with the least number of connected components, smallest maximum width, and height is selected as the most compact.
Compliance Function Steps:
- Predicate Check: Ensure each chord forms a connected graph.
- Trajectory Calculation: Build trajectories in all candidate Tonnetz.
- Compactness Evaluation: Measure the width, height, and number of connected components of each trajectory.
- Normalization and Selection: Normalize values and select the Tonnetz with the highest compactness score.
Graph Representation Centrality Measures and Future Possibilities
Once a trajectory is constructed, it is transformed into a weighted graph. Each chord becomes a vertex, and edges represent the connections based on the Tonnetz intervals. Centrality measures (Katz, harmonic, closeness) are then calculated to capture the structural properties of the graph. These centrality measures, along with the general MIDI descriptors, form the feature set for classification algorithms, such as Random Forest and k-Nearest Neighbors.
Furthermore, the graph representation of harmonic trajectories in the Tonnetz opens a gateway to advanced deep learning methods, particularly leveraging graph neural networks (GNNs). By transforming musical sequences into weighted, non-directed graphs, where vetrices model notes and edges their configuration in the Tonnetz space, this method enables the use of GNNs to learn intricate relationships within the music data. GNNs can effectively model the dependencies and patterns in these graph structures, allowing for potential improvements on classification tasks. This deep learning approach can uncover latent harmonic features and complex interactions that traditional methods might miss, providing a more robust framework for tasks such as composer classification, tonal tension, and even compositional style analysis.
Conclusion
The Tonnetz-based trajectory method offers a powerful tool for harmonic analysis and genre classification in music. By representing chords and their transitions in a geometric space, this method provides a nuanced understanding of harmonic relationships. The compliance function and centrality measures ensure that the trajectories are both compact and informative, leading to high classification accuracy.
Future work will explore applying geometrical deep learning techniques, such as graph convolutional networks (GCNs) and graph attention networks (GATs), to further enhance the analysis and classification of harmonic trajectories. By leveraging these advanced models, we aim to capture the complex, non-Euclidean relationships inherent in musical compositions, enabling more precise and insightful characterizations of musical styles and genres. This approach may provide deeper insights into the underlying harmonic structures and stylistic nuances of different musical pieces.